In the world of algebra, equations can feel like cryptic puzzles waiting to be solved. Take the equation 61 = -9c + 7. At first glance, it might seem like a riddle only a math wizard could crack. But fear not! This equation is more approachable than it appears, and diving into its depths can be surprisingly fun.
Table of Contents
ToggleOverview of the Equation
The equation 61 = -9c + 7 represents a linear relationship that can be solved for the variable c. Simplifying provides clearer insights into its structure and solutions. Begin by isolating the variable c to understand its implications fully.
First, subtract 7 from both sides to eliminate constants on the right side. This transforms the equation into 61 – 7 = -9c. The result simplifies to 54 = -9c. Next, divide by -9 to find the value of c. The simplified equation shows that c = -6.
Linear equations like this one often serve as fundamental tools in algebra. Recognizing similar structures in various equations leads to efficient problem-solving strategies. Mathematics thrives on solving for unknowns, making equations valuable in real-world applications like finance or engineering.
Identifying each component of the equation supports a clear understanding of its function. Constants, coefficients, and variables play distinct roles in determining outcomes. Mastering these relationships enhances proficiency in algebra, encouraging further exploration of mathematical concepts.
Solving linear equations cultivates critical thinking and analytical skills. Engaging with the equation 61 = -9c + 7 serves as an effective introduction to algebraic principles. Through practice, individuals can develop the confidence needed to tackle more complex mathematical challenges.
Analyzing the Components of 61= −9c+7
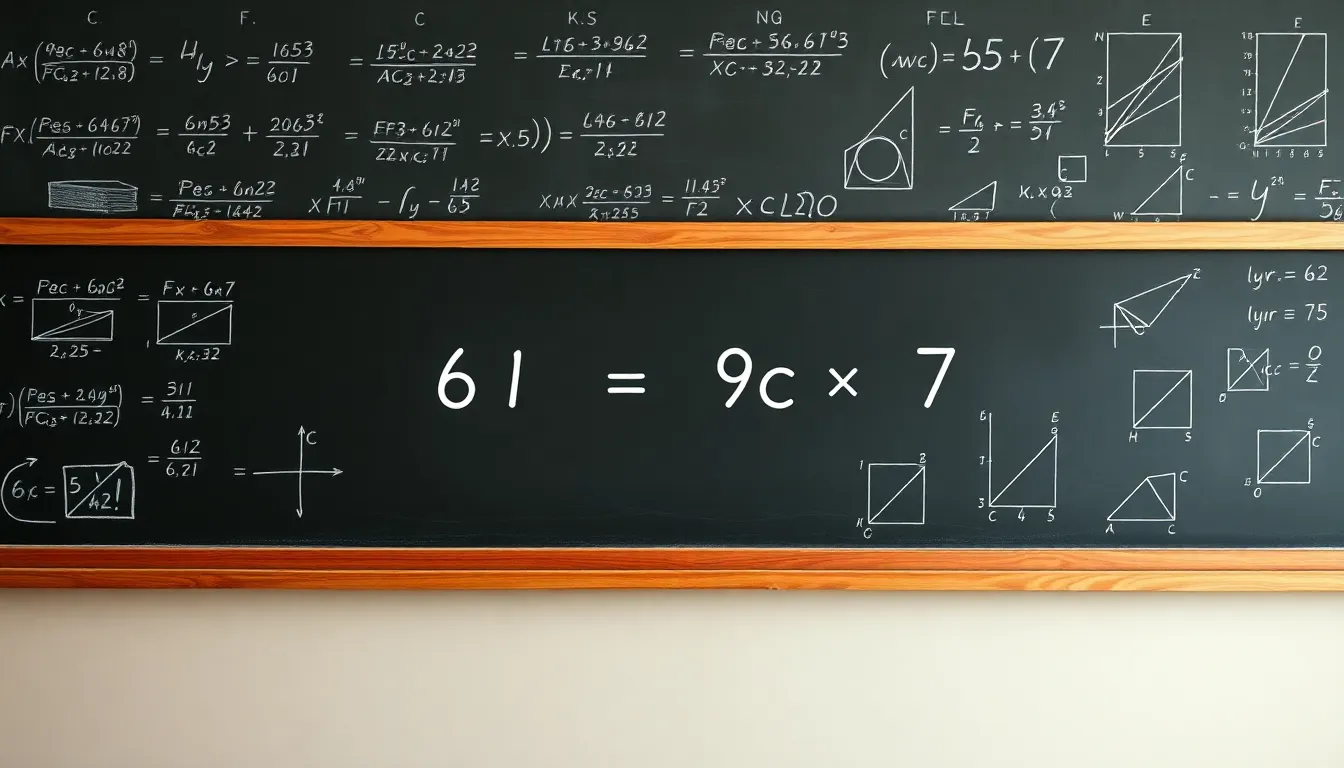
Examining the components of this equation reveals essential algebraic concepts that aid in understanding its structure.
Understanding Constants and Coefficients
Constants play a crucial role in the equation. In 61 = −9c + 7, the constants are 61 and 7. These values remain unchanged regardless of the variable’s value. Coefficients, on the other hand, are the multipliers of variables. Here, the coefficient is -9, which affects the variable c by scaling its value. Knowing how these elements interact helps clarify their influence in algebraic expressions. Identifying constants and coefficients assists in solving equations effectively and simplifies the problem-solving process.
The Role of Variables in the Equation
Variables represent unknown values and are fundamental to algebraic equations. In this case, c is the variable that needs isolation to solve the equation. Understanding its function helps in recognizing the relationship to other components. The value of c changes based on the equation’s constants and coefficients. Manipulating variables effectively leads to solutions and insights within a mathematical context. Recognizing the role of variables can enhance problem-solving skills and boosts overall algebraic comprehension.
Solving the Equation
Solving the equation 61 = -9c + 7 involves following a structured approach. First, isolate the variable c by performing basic arithmetic operations.
Step-by-Step Solution Process
- Subtract 7 from both sides: This action yields 61 – 7 = -9c.
- Calculate the left side, resulting in 54 = -9c.
- Divide both sides by -9: By doing this, c equals 54 / -9.
- Result in c = -6. Each step clarifies the process of isolating the variable effectively.
Common Mistakes to Avoid
Missteps often occur during the subtraction phase. Forgetting to subtract 7 from both sides can lead to inaccurate results. Division mistakes also arise when calculating values, especially with negative signs. Incorrectly handling negative numbers creates confusion, leading to erroneous conclusions about c. Always double-check each step to ensure accuracy and prevent common pitfalls in basic algebra.
Applications of the Equation
The equation 61 = -9c + 7 serves various practical purposes. In fields like economics, it can model cost functions where c represents quantities that directly affect total costs. This allows analysts to predict changes in costs as production levels fluctuate.
Engineers use similar equations to optimize designs. The relationship established by the equation helps determine load capacities and material stresses, ensuring safety and efficiency in structures. Rather than relying solely on empirical data, they apply algebraic processes to simulate various scenarios.
Businesses also benefit from solving such equations. Pricing strategies can be informed by understanding relationships between production costs and sales prices. Adjustments in c reflect changes in market conditions, allowing businesses to remain competitive.
Education often incorporates this equation to teach algebraic principles. Learners engage with the concept of linear relationships through relatable examples. They gain confidence in problem-solving skills, applying them in math and science contexts.
Additionally, data scientists find value in rearranging equations like 61 = -9c + 7. They analyze correlations within datasets, identifying trends that assist in making data-driven decisions. Clarity in understanding variable relationships leads to more accurate predictions.
Healthcare professionals also utilize these equations in their analyses. By assessing resource allocation and patient care costs, they make informed decisions that impact operational efficiency. The equation helps break down complex relationships into understandable formats.
Overall, linear equations form the backbone of numerous disciplines. Applying techniques to solve these equations fosters critical thinking and enhances analytical capabilities.
Mastering the equation 61 = -9c + 7 opens the door to a deeper understanding of algebra. By isolating the variable c, individuals not only solve the equation but also enhance their problem-solving skills. Recognizing the roles of constants and coefficients simplifies complex concepts and builds confidence.
The practical applications of such equations span various fields, demonstrating their value beyond the classroom. Whether in economics engineering or healthcare these linear relationships play a crucial role in decision-making processes. Embracing algebraic principles equips individuals with essential analytical tools that can be applied in real-world scenarios.













